MENTAL vs. Conceptografia de Frege

MENTAL vs.
CONCEPTOGRAFÍA
DE FREGE

“La aritmética ha sido el punto de partida del tren de pensamiento que me ha conducido a mi Conceptografía” (Frege)

“Los componentes primitivos se deben tomar tan simples como sea posible si se ha de producir orden y claridad” (Frege)

“Cuando Frege introdujo la cuantificación, iluminó tres temas: lógica, lenguaje y ontología” (Quine)

La Conceptografía de Frege
Gottlob Frege −considerado el mayor lógico desde Aristóteles− es el padre de la lógica moderna (la lógica matemática) y de la filosofía analítica (la filosofía basada en el análisis lógico del lenguaje). En 1879 (con 31 años) publicó una obra revolucionaria titulada “Begriffsschrift” (Conceptografía, Ideografía, notación conceptual o escritura conceptual), subtitulada “Un lenguaje en fórmulas del pensamiento puro, a imitación de la aritmética” [Frege, 1972]. En ella presentó una nueva notación lógica para representar conceptos y proposiciones, así como nuevos conceptos, entre ellos los predicados y los cuantificadores lógicos. Fue su primer y revolucionario texto sobre lógica matemática, iniciando una nueva era en lógica, una disciplina que había permanecido prácticamente inalterada desde Aristóteles. A su vez, esta obra era un intento de crear un lenguaje universal, preciso y formalizado para su aplicación en ciencia y filosofía.

En el prefacio de esta obra, Frege señala que el sistema presentado en ella era la realización del sueño de Leibniz de un lenguaje universal para la ciencia, un lenguaje en el que los conceptos y las verdades de la ciencia podrían expresarse con precisión de manera simbólica. Pero en esta obra solo bosquejó su sistema. Un sistema más elaborado apareció en los dos volúmenes de Grundgesetze der Arithmetik (Las Leyes Básicas de la Aritmética), publicados, respectivamente, en 1893 y 1903.

La filosofía de Frege

Logicismo.
Frege era defensor del logicismo, la idea de que la matemática es reducible a la lógica, por ser la lógica lo más abstracto que existe y que conecta con las leyes más profundas del pensamiento. Pero su defensa del logicismo se limitó a la aritmética. Su obra “Las Leyes Básicas de la Aritmética” fue el registro del intento de su proyecto logicista.

Para llevar a cabo su proyecto logicista, Frege desarrolló como fundamento una doctrina semántica, con una serie de nociones clave y que reflejó en tres artículos: “Función y Concepto” (1891), “Sobre sentido y referencia” (1892) y “Sobre concepto y objeto” (1892).

Su proyecto logicista fracasó finalmente por su inconsistencia, por la famosa paradoja de Russell. Durante la última etapa de su vida, Frege abandonó el logicismo y realizó un giro kantiano, al intentar demostrar que la aritmética (y la matemática en general) debería fundamentarse sobre la geometría y no sobre la lógica. Su intento quedó inconcluso debido a su muerte en 1925.
Rechazo del psicologismo.
Frege rechazó el psicologismo en lógica y matemática. El psicologismo (o subjetivismo) es la visión de que todo conocimiento son solo ideas subjetivas abstraídas de la experiencia individual. El psicologismo matemático sostiene que los objetos matemáticos (como los números) son abstracciones de la experiencia sensible. El psicologismo lógico son solo leyes del “recto pensar”. El filósofo empirista John Stuart Mill fue el más destacado entre los psicologistas por llevar su concepción al extremo de considerar a la matemática y la lógica como disciplinas subordinadas a la psicología.

Frege distinguía entre las leyes del pensar psicológico y las leyes de la lógica. El objeto de estas últimas es investigar la verdad, el ser verdadero.
El Tercer Mundo.
Logicismo y anti-psicologismo se enmarcan en la teoría de Frege de los tres mundos. Según Frege, existen tres mundos o reinos: 1) el mundo físico objetivo y sensible; 2) el mundo de las ideas, los procesos mentales y las representaciones psicológicas, de tipo subjetivo; 3) el mundo de los conceptos y entidades de tipo lógico, un mundo objetivo y atemporal que es independiente de las mentes subjetivas individuales. Por ejemplo, los números son entidades de tipo lógico que residen en el Tercer Mundo, que son independientes de todo proceso y representación psicológicos.

Para Frege, las expresiones formales abstractas tienen significado, son objetivas y pertenecen al Tercer Mundo. Rechazó el formalismo de la aritmética, según el cual el número y las expresiones aritméticas son un mero juego de símbolos sin significado, sin sentido. Con la idea del Tercer Mundo, Frege se alineó con el realismo platonista.

Características generales de la Conceptografía

Lenguaje universal.
Frege pretendía crear, siguiendo el espíritu de Leibniz, una Lingua Characteristica Universalis y no un mero Calculus Ratiotinator. El lenguaje debería ser universal en el sentido de que el universo del discurso fueran todas las cosas, un lenguaje que permitiría conectar en un solo dominio campos que antes estaban separados y que podría extenderse a campos que necesitasen un lenguaje formal.

Frege fue el primer autor en la historia en intentar crear un lenguaje universal formalizado para la ciencia. Anteriormente, Descartes (con su Mathesis Universalis) y Leibniz (con su Lingua Characteristica) lo intuyeron, pero no consiguieron hacerlo efectivo. Frege fue el primero en intentarlo seriamente. Siguiendo la filosofía de Leibniz, utilizó símbolos para expresar conceptos elementales y combinaciones de estos símbolos para expresar conceptos compuestos.
Lenguaje lógico ideal.
Frege fue un universalista que buscaba a través de la lógica la unificación de matemática, lingüística, filosofía y la estructura de la realidad. Para Frege, el fin de la lógica no es calcular (realizar inferencias), sino modelar y comprender la realidad. Para ello creó un lenguaje lógico ideal, la Conceptografía, un lenguaje formal para el “pensamiento puro”. El pensamiento puro se basa exclusivamente en formas generales, prescindiendo de todo contenido particular.

El lenguaje natural es ambiguo, poco adecuado para la ciencia y la filosofía, por lo que Frege se animó a crear un lenguaje preciso, un lenguaje de fundamento puramente lógico, un lenguaje formal perfecto. Su primera aproximación a este lenguaje formal ideal fue intentar formalizar la aritmética mediante la lógica, porque creía que las entidades aritméticas eran entidades lógicas. Al hacerlo, se percató de que los conceptos que manejaba eran generales, que iban más allá de la aritmética, por lo que extendió su sistema a la representación de conceptos de todo tipo y no solo matemáticos, por lo que finalmente creó un lenguaje aplicable a las ciencias formales en general. “La aritmética fue el punto de partida del tren de pensamiento que me condujo a la Conceptografía”. Frege fue un lógico que vio en la lógica el paradigma universal que le permitiría crear un lenguaje universal. Esta idea de la lógica como fundamento del lenguaje perfecto sería seguida posteriormente por Russell para intentar también fundamentar la matemática.
Lenguaje analítico.
Kant mantenía que la geometría y la aritmética son ciencias sintéticas a priori, que requieren de la intuición. Frege quería demostrar que la aritmética es analítica, es decir, que sus conceptos fundamentales son de tipo lógico exclusivamente, por lo que toda la aritmética se podría definir en términos puramente lógicos, reducirlo a leyes lógicas.
Lenguaje axiomático.
Frege quería establecer un sistema axiomático formal para la aritmética, como en la geometría de Euclides. A partir de un conjunto reducido de axiomas se podrían derivar la totalidad de las verdades (teoremas) de la aritmética. Posteriormente este sistema se extendería a todas las matemáticas.

Frege formalizó la noción de demostración en términos que hoy siguen vigentes: una demostración es una secuencia finita de sentencias tales que cada una de ellas es un axioma o se sigue de las anteriores por una regla de inferencia válida.
Lenguaje científico.
En el prefacio de su Conceptografía, Frege afirma que este lenguaje se puede extender a otras ciencias que requirieran un lenguaje formal, añadiendo conceptos y axiomas específicos de cada dominio. El lenguaje sería especialmente aplicable en especial a la geometría y a la física. “El paso a la teoría del movimiento puro, y aún a la mecánica y a la física, podrían seguirse de aquí” [Frege, 1972].
Lenguaje simple.
Frege buscó conceptos lógicos primitivos de la máxima simplicidad y en el menor número posible. A partir de esos conceptos primarios fundamentales, por combinatoria, se construirían los conceptos derivados, compuestos y complejos. “Los componentes primitivos se deben tomar tan simples como sea posible si se ha de producir orden y claridad” [Frege, 1972]. “... nuestro esfuerzo ha de ser prácticamente retroceder hasta lo lógicamente simple, que en cuanto tal no es propiamente definible” [Frege, 2003].
Conceptografía como ciencia.
Frege sostenía que su sistema de Conceptografía era más que una Lingua Characteristica y un Calculus Ratiotinator. Que era una verdadera ciencia en sí misma, donde cada teorema de esta ciencia se podía demostrar mediante sus conceptos primarios y sus axiomas lógicos fundamentales
Lenguaje creativo.
Frege no solo pretendía crear un lenguaje simbólico que reflejase los conceptos (y sus relaciones) ya existentes, sino que también debería permitir la formación de nuevos conceptos y nuevas relaciones. Frege creía que su notación conceptual podría ayudar a la filosofía a romper el dominio de la palabra sobre la mente para intentar capturar lo profundo, lo oculto en el lenguaje natural.
Filosofía analítica.
Frege quería que su lenguaje no fuera una herramienta meramente descriptiva, sino una herramienta de análisis científico-filosófico del lenguaje ordinario, para ayudar a detectar lo que está oculto o implícito, para superar sus deficiencias y ambigüedades, y para buscar sus conceptos esenciales y sus relaciones. Esta línea de investigación se denominaría posteriormente “filosofía analítica”.
Un lenguaje distinto del álgebra de Boole.
La Conceptografía se diferencia del álgebra de Boole en tres aspectos:
1. Lenguaje.
  El álgebra de Boole funciona solo como un Calculus Ratiotinator. El lenguaje de Frege pretendía ser además una Lingua Characteristica Universalis en el sentido de Leibniz, un lenguaje universal.
2. Relación entre matemática y lógica.
  Boole realizó un análisis matemático de la lógica. Frege procedió a la inversa: pretendía basar toda la matemática en la lógica, pues sostenía que la lógica no depende de la matemática, sino que es la matemática la que deriva de la lógica.
3. Semántica.
  El cálculo lógico de Boole es formal, sintáctico. La proposición no tiene contenido, es vacía, y su semántica está reducida a un mero valor de verdad. En cambio, con Frege, toda proposición tiene raíces filosóficas: tiene estructura y contenido conceptual, es decir, tiene asociado un sentido, un significado. El álgebra de Boole creó un simbolismo para conceptos ya existentes. La Conceptografía creó nuevos conceptos y una nueva simbología.
  
  Por lo tanto, el poder expresivo de la Conceptografía es superior al álgebra de Boole.

Principios generales

El principio de composicionalidad.
El significado de una expresión compuesta viene determinado por el significado de sus componentes y las relaciones entre ellos. Si se cambia un componente por otro de distinto significado, cambia el significado de la sentencia.
Sentido y referencia.
Son los dos conceptos más importantes de la filosofía de Frege, aunque todavía hoy son temas debatidos, especialmente el concepto de “sentido”. Sentido y referencia son dos aspectos distintos del significado. El sentido de una expresión es su forma y su contenido. La referencia es el objeto al que hace referencia la expresión.

La referencia de una proposición es su valor de verdad. La referencia de todas las proposiciones verdaderas es lo Verdadero, y la referencia de todas las proposiciones falsas es lo Falso. Dos expresiones diferentes tienen distinto sentidos, pero pueden tener la misma referencia. Por ejemplo, 22 y 1+3, tienen diferente sentido y la misma referencia, 4. No todo sentido tiene referencia.
El principio del contexto.
Sólo en el contexto de una proposición como un todo conocemos los significados de las palabras que la componen. Las palabras aisladas no tienen referencia, la tienen los enunciados completos.
Conexión entre pensamiento y lenguaje.
Según Frege, existe una estrecha conexión entre los elementos de un pensamiento y la oración que la expresa, aunque dos oraciones distintas pueden expresar el mismo pensamiento. A nivel lingüístico, es una correspondencia entre sintaxis y semántica.
Uso y mención.
Frege distingue entre “uso” y “mención” de una expresión. El uso hace referencia al objeto designado. La mención hace referencia a la propia expresión (la expresión material o formal).

Caracteríticas detalladas de la Conceptografía

Funciones y objetos.
La ontología de Frege consta de dos tipos de entidades fundamentales: funciones y objetos. Una función es una entidad “no saturada”, es decir, incompleta, con una o más variables que tienen que ser completadas con sus correspondientes argumentos (objetos) para su “saturación”. Un objeto es una entidad “saturada” (completa). Dentro de los objetos se incluyen los valores lógicos Verdadero) y Falso.

Según Frege, la gramática ordinaria ha entorpecido el desarrollo científico. En este sentido, sustituye los conceptos gramaticales de sujeto y predicado por los de argumento y función., por ser éstos conceptos más generales y flexibles.

Frege tomó los conceptos de función y argumento de la matemática, pero los generalizó para aplicarlos a enunciados: una función es un enunciado en el que aparecen una o más variables. Cuando se asignan valores a las variables (los argumentos), hay un enunciado resultante, que puede ser verdadero o falso. Un ejemplo de función es “x es un planeta del sistema solar”, en donde x es la variable que puede admitir diferentes argumentos. Si x=Tierra, el enunciado es verdadero. Si x=Luna, el enunciado es falso.

El conjunto de argumentos (objetos) que hace verdadera a una función se denomina “recorrido” o “curso” de dicha función. En el ejemplo de la función anterior, su recorrido es “Mercurio, Venus, Tierra, Marte, Júpiter, Saturno, Neptuno y Urano”. Si dos funciones tienen el mismo recorrido son iguales entre sí.

En una expresión, el que una parte sea argumento y la otra función depende del punto de vista que se elija. Por ejemplo, en “Pedro golpeó a Marco”, se puede considerar como la función “x golpeó a Marco” con x=Pedro, o como la función “Pedro golpeó a x” con x=Marco. Incluso se podría considerar la función de dos variables “x golpeó a y”, con x=Pedro e y=Marco.
Variables y constantes.
Frege distingue entre variables y constantes. La variables (simbolizadas por letras) pueden representar diferentes contenidos en diferentes ocasiones. Esto permite expresar leyes generales, como la ley conmutativa de la suma: x+y = y+x. Hay variables relativas a objetos y variables relativas a funciones.

Las constantes (que son símbolos especiales) tienen un significado completamente determinado como el número 12 o los operadores aritméticos “+” y “−”.
Conceptos.
Un concepto es un tipo especial de función. Un concepto es una función que mapea todos los argumentos a un valor de verdad. Por ejemplo, x>2 define el concepto de ser mayor que 2. Si x=5, la sentencia es verdadera y si x=1, la sentencia es falsa.

Otro ejemplo es la función “x conquistó las Galias”, que es un concepto porque se pueden asignar valores a x y el resultado es una sentencia verdadera o falsa. Si x=César, la sentencia es verdadera , y si x=Galileo, la sentencia es falsa.

Un objeto que hace que el concepto sea verdadero se dice que “cae” bajo ese concepto. Por ejemplo, el objeto 3 cae bajo el concepto x>2, el objeto 2 cae bajo el concepto x²=4, y el objeto 5 cae bajo el concepto P(x) que indica “x es primo”.
Extensión de un concepto.
La extensión de un concepto es el conjunto de objetos que caen bajo ese concepto. Por ejemplo, la extensión del concepto “azul” es el conjunto de todas las cosas azules, la extensión del concepto “3” es el conjunto de los objetos constituidos por 3 elementos, la extensión del concepto “verdad” es el conjunto de todos los objetos verdaderos, la extensión del conjunto “primo” es el conjunto de los números primos, la extensión del concepto “>2” son los números 3, 4, 5, etc.
Predicación como aplicación funcional.
La predicación es un caso particular de aplicación funcional. Por eso se utiliza la notación funcional, como en P(x) (x es primo). Así que un predicado es una función que mapea sus argumentos a un valor de verdad. Por ejemplo si M(x, y) representa el predicado “x es mayor que y”, entonces M(5, 3) es verdadero y M(3, 5) es falso. Por lo tanto, un predicado es un concepto, y éste se formaliza como una función.
Conceptos lógicos.
Frege utiliza los conceptos lógicos siguientes:
1. Juicio.
  Un juicio (aserto, aserción o afirmación) se expresa con el símbolo “⊢“ a la izquierda de una expresión. Los juicios son afirmaciones o teoremas (deducciones). El símbolo consta de una barra vertical y otra horizontal. La barra horizontal (barra de contenido) indica un contenido: es una mera combinación de conceptos a modo de representación, pero no un juicio. La barra vertical (barra de juicio) indica un juicio, una afirmación. Los juicios pueden ser particulares o universales. Un ejemplo de juicio particular es ⊢3×7 = 21. Un ejemplo de juicio general es ⊢a+b = b+a.
  
  Todos los juicios (que están representado por el símbolo ⊢) indican el mismo predicado: “es el caso”, “es un hecho” o “es verdad”. Por ejemplo, “Arquímedes pereció en la toma de Siracusa” se transforma (al incluir el símbolo de juicio) en “Es un hecho la muerte de Arquímedes en la toma de Siracusa”.
2. Condición.
  Usa el símbolo siguiente:
  
  La barra horizontal es la barra de contenido, y la barra vertical es la barra de condición. Se define como implicación material: “Si B entonces A”, siendo B el antecedente y A el consecuente, y sin que haya necesidad de relación causal entre A y B. Equivale en notación moderna a A→B. Esta es la única regla de inferencia (el modus ponens). Los demás modos de inferencia se reducen al modus ponens. Es la única regla que se utiliza para derivar todas las verdades aritméticas. “Puesto que es posible salir adelante con un solo medio de inferencia, entonces es un precepto de claridad hacerlo así” [Frege, 1972].
3. Negación.
  Se simboliza por una pequeña barra perpendicular (barra de negación) a la barra de contenido en su parte inferior, que indica que el juicio no tiene lugar:
  
  Equivale en notación moderna a ¬A.
4. Función.
  Se utiliza la notación ⊢Φ(A) para una función de un argumento (A) y ⊢Φ(A, B) para una función de dos argumentos (A y B). La expresión Φ(A) también se puede concebir como una función de argumento Φ, puesto que Φ podría reemplazarse por otro símbolo.
5. Igualdad de contenidos.
  Simbolizado por: ⊢A≡B, es una identidad de referencia y no una igualdad entre símbolos, es decir, se trata de “uso” y no de “mención”. Indica que el contenido de B puede sustituir a A.
6. Generalidad.
  Se utiliza un símbolo formado por una línea horizontal con una concavidad en cuyo interior se coloca una letra). Sirve para cuantificar variables individuales y funciones. Por ejemplo,
  
  es la ley de la conmutatividad de la suma.
  
  Otro ejemplo es
  
  que es una función de segundo orden que mapea G a V si G mapea todo objeto a V. En caso contrario, mapea a F.
  
  Una letra latina indica una variable no cuantificada y tiene como dominio el contenido del juicio completo. Si aparece una letra latina en una expresión a la que no preceda una barra de juicio, entonces la expresión carece de sentido.
7. Definición.
  Se utiliza la notación : ||—A≡B. Sirve para establecer una definición donde el símbolo A representa al contenido de B.
Axiomas lógicos.
Frege declaró 9 de sus proposiciones como axiomas. Lo justificó porque expresan verdades intuitivas. Todas las demás propiedades se deducen de estos 9 axiomas y una única regla de inferencia (el modus ponens). El axioma 7 es de la lógica de predicados de segundo orden. En notación moderna, estos axiomas son:

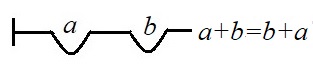
Nº	Axioma
1	A→(B→A)
2	[A→(B→C)] → [(A→B)→(A→C)]
3	[D→(B→A)] → [B→(D→A)]
4	(B→A) → (¬A→¬B)
5	¬¬A → A
6	A → ¬¬A
7	((c≡d) → ∀f ( f(c)→f(d) ))
8	c≡c
9	∀a(f(a)) → f(c)

MENTAL vs. Conceptografía
Entre la Conceptografía y MENTAL hay más que analogías; hay coincidencias, aunque también hay diferencias:

Características generales

Motivación y objetivos.
La Conceptografía nació inicialmente como un medio para clarificar y formalizar los conceptos aritméticos mediante conceptos lógicos. Posteriormente Frege creyó ver características universales en su lenguaje.

MENTAL fue creado inicialmente con el objetivo de de crear un lenguaje unificado para la informática. Pero pronto se vio que las primitivas, por su alto nivel de abstracción, tenían una aplicación universal, que servía para fundamentar (a nivel teórico y práctico), no solo la informática, sino también la matemática y las ciencias formales en general.
Universalidad.
Frege no aclara cual es el fundamento de su lenguaje para ser considerado como universal. Además, el lenguaje de Frege no es suficientemente general, no es universal, porque está restringido a la lógica de predicados de segundo orden, y un lenguaje universal no debería tener restricciones.

MENTAL basa su universalidad en los arquetipos primarios, los arquetipos de la conciencia. Es un lenguaje sin restricciones, pues los arquetipos primarios son grados de libertad.
Fundamentación.
La Conceptografía se basa en la lógica exclusivamente. Frege lo justificaba en que como la finalidad de la ciencia es la búsqueda de la verdad, la lógica tenía que ser el fundamento del lenguaje universal para la matemática y para la ciencia en general. El modo más firme de sustentación de una verdad científica es su demostración lógica. Todo conocimiento debe basarse en la lógica. “La tarea de la lógica es descubrir las leyes de la verdad, no las leyes de la afirmación o del pensamiento”. Paradójicamente, afirmaba que la verdad es indefinible.

Frege realiza una mezcolanza de doctrina semántica y definiciones lógicas. MENTAL utiliza primitivas semánticas, de las cuales solo una (la Condición) es de tipo lógico, que sirve como fundamento de la lógica de decisión y de implicación.
Lenguaje ideal.
La Conceptografía pretendía ser un lenguaje ideal para superar las limitaciones del lenguaje ordinario, un lenguaje basado en el “pensamiento puro”.

MENTAL va en el mismo sentido, pues lo que Frege denomina “pensamiento puro” se puede interpretar como arquetipos, pues según Jung, los arquetipos son formas sin contenido. Podríamos decir que Frege, buscaba, más o menos conscientemente, los arquetipos primarios, lo más profundo de la realidad, y creyó que esos arquetipos eran de tipo lógico. Pero la lógica no es el fundamento profundo de la realidad. Es solo una de las dimensiones de la realidad.
Lógica de predicados.
Frege considera a los predicados como funciones que se mapean a valores de verdad. La lógica de predicados de Frege es de “segundo orden”, pues permite la cuantificación de funciones. Por ejemplo, en notación moderna, el axioma (a≡b → ∀F(Fa→Fb)).

En MENTAL, los predicados son de carácter general, no ligados exclusivamente a la lógica. La predicación es una particularización de una expresión, que incluye en particular el concepto de atributo o predicado, de notación x/y (y particulariza a x). La predicación es un concepto diferente de función; es una relación entre objetos, aunque también puede utilizarse como función. Por ejemplo,
Los predicados se pueden aplicar a cualquier tipo de expresión. Y puede ser de cualquier orden, no hay límite.
Filosofía.
La Conceptografía se considera que marcó el comienzo de la filosofía analítica, pues Frege concibió un lenguaje filosófico. Frege quiso hacer de la lógica la disciplina fundacional de la filosofía.

Los conceptos primarios de MENTAL son, además de arquetipos primarios, categorías filosóficas. MENTAL es un lenguaje filosófico.
Psicología.
Para Frege, la tarea de la matemática y de la lógica no es investigar los contenidos mentales individuales subjetivos, pero admitía que quizás la tarea de ambas disciplinas es investigar la mente en general.

Los arquetipos primarios de MENTAL constituyen un modelo de la mente y de la conciencia.
Simplicidad.
Frege buscó los conceptos lógicos de la máxima simplicidad y en el menor número posible.

MENTAL se basa en conceptos simples de suprema abstracción: las primitivas semánticas universales, de las cuales solo una es una primitiva lógica (la Condición).
Ciencia.
Frege sostenía que la Conceptografía era una ciencia en sí misma.

MENTAL es también una ciencia en sí misma, pero no una ciencia más, sino una meta-ciencia, o ciencia universal, pues es el fundamento de las ciencias formales.
Axiomas.
Frege utiliza 9 axiomas lógicos, formalizados en la Conceptografía. En “Las leyes básicas de la aritmética” utilizó un axioma −el V concretamente, el axioma de la doble negación−, que trata de la extensión de un concepto, axioma que se demostró que era inconsistente. El axioma V implica una contradicción, como señalo Russell en una carta a Frege: hay conceptos cuyas extensiones incluyen a los propios conceptos.

Hoy se reconoce que Frege demostró que aritmética es reducible a la lógica de segundo orden extendida por el principio de Hume. Este principio dice: “Dados dos conceptos F y G, el número de Fs es igual al número de Gs si y solo si hay correspondencia uno a uno entre los Fs y los Gs. Esto se expresa mediante el llamado “Teorema de Frege”: Todos los principios fundamentales de la aritmética son derivables del principio de Hume como único axioma, junto con las definiciones de “0”, “sucesor” y “número natural” en el seno de la lógica de segundo orden en la que se admiten variables que varían sobre conceptos, no solo elementos de un conjunto.

MENTAL se basa en 12 axiomas semánticos, que son primitivas semánticas universales o arquetipos primarios. También utiliza axiomas generales que relacionan las primitivas. No se considera la cuestión de la consistencia, pues este tema está asociado a la verdad y falsedad, y en MENTAL la verdad no es intrínseca, sino extrínseca: lo verdadero (V) y lo falso (F) son constantes que se pueden utilizar en las expresiones (como atributo, como magnitud lógica, etc.). La verdad es indefinible, como afirmaba Frege. MENTAL no se basa en la noción de verdad, sino en la noción de existencia de una expresión en el espacio abstracto.
Tipo de lenguaje.
El lenguaje de Frege es descriptivo y normativo (sobre cómo realizar inferencias). Pero no es operativo, no se pueden definir procesos.

MENTAL es un lenguaje descriptivo y operativo. Y las inferencias son automáticas.
Principio de composicionalidad. Frege definió el principio de composicionalidad.

En MENTAL, la composicionalidad se basa exclusivamente en las primitivas. La semántica estructural es la misma que la semántica lexical.
Notación.
La Conceptografía es un lenguaje gráfico bidimensional. MENTAL es lineal, unidimensional.

Frege introdujo una nueva notación original, aunque era muy compleja. Hoy día se usa una más fácil y comprensible, desarrollada por Peano y adoptada por Russell (se denomina “notación Peano-Russell”) que se utilizó en la obra Principia Mathematica (de Russell y Whitehead), inspirada en el logicismo de Frege. MENTAL, a su vez, simplifica y generaliza la notación de Peano-Russell.
Analítico vs. sintético.
Desde que Kant formulara la distinción entre juicios analíticos y sintéticos, los filósofos han intentado clarificar la distinción en general entre los conceptos “analítico” y “sintético”, sin que se haya logrado un consenso general. Aquí vamos a definir estos dos conceptos de la manera más simple (siguiendo el principio de la navaja de Occam), sobre la base de los dos modos de conciencia. Lo sintético es lo intuitivo, necesario, universal y a priori. Lo analítico es lo racional, lo contingente, particular y a posteriori.

En este sentido, los principios de la matemática (incluyendo la aritmética) son sintéticos: son de tipo intuitivo, universales, necesarios y a priori. Todas las primitivas de MENTAL son sintéticas (se basan en la intuición), a priori (previas a la experiencia), universales y necesarias. Todo lo demás (derivadas y expresiones) son analíticas (se basan en el razonamiento), a posteriori, particulares y contingentes.
Tercer Mundo.
Frege era platonista. Decía que las entidades abstractas las y verdades lógicas y matemáticas tienen una existencia real, independiente de nuestros contenidos mentales y que habitan en un “Tercer Mundo”, un mundo objetivo que trasciende lo físico y lo mental.

Las primitivas de MENTAL son arquetipos primarios, un concepto equivalente a las Ideas platónicas. Los arquetipos primarios son inexpresables y trascendentes, de los que solo podemos ver sus manifestaciones concretas. Las expresiones de MENTAL, que son manifestaciones de los arquetipos primarios, se pueden considerar que residen en un tercer mundo de entidades abstractas, pues no son ni físicas ni mentales.
Otras lógicas.
Frege no exploró otras lógicas, como la lógica modal (la que trata las cuestiones de necesidad y posibilidad) y la lógica temporal (la lógica en la que intervienen los tiempos verbales). MENTAL es un lenguaje en el que todo concepto lógico (lo modal, lo temporal, lo borroso, etc.) se generaliza, es decir, no van ligados exclusivamente a la lógica.
Aplicación a otras ciencias.
Frege decía que su lenguaje podía extenderse a otras ciencias, como la geometría y a la física, añadiendo conceptos y axiomas específicos de estos dominios.

MENTAL se puede aplicar directamente a la geometría como geometría analítica y álgebra geométrica, sin añadir nuevos conceptos. Y MENTAL es un lenguaje aplicable a la física clásica, moderna y computacional (o digital).
Cálculo diferencial e integral.
Frege confiaba en que la Conceptografía serviría para fundamentar el cálculo diferencial e integral. No fue así.

MENTAL permite definir de manera increíblemente sencilla el concepto de infinitésimo (ε*ε=0) y, partir de él, el cálculo diferencial e integral.
Paradojas.
El sistema formal de la aritmética de Frege resultó al final inconsistente, con la aparición de la paradoja de Russell.

En MENTAL no hay paradojas. Hay expresiones fractales.

Características de detalle

Función y argumento.
En la Conceptografía, la función es un concepto fundamental. Pero las funciones solo son patrones de proposiciones y no pueden realizar procesos. Son solo descriptivas.

En MENTAL, función es un concepto derivado. Aunque existen muchas formas de implementación, normalmente se implementa mediante una expresión genérica con parámetros. En MENTAL se diferencia claramente entre parámetros y argumentos (los valores concretos de los parámetros). Las funciones pueden realizar procesos.
Número.
Según Frege, los números atañen a los conceptos y no a las cosas. Definió el número de un concepto F como el conjunto de todos los conjuntos que son equinumerables con F. El número 0 se define como el número asociado al concepto de “no ser idéntico a sí mismo”.

Pese a todos los esfuerzos de Frege,el concepto de número es indefinible. En MENTAL, el número está basado en la primitiva semántica “Suma”, que es indefinible (como todas las primitivas); solo podemos ver sus manifestaciones.
Sentido y referencia.
Estos dos conceptos tienen en MENTAL una interpretación simple: el sentido de una expresión es la propia expresión, que tiene un significado basado en las primitivas semánticas. La referencia es el resultado de su evaluación, que puede corresponder a una entidad mental abstracta o a un objeto físico. Cuando una expresión se autoevalúa, sentido y referencia coinciden.
Uso y mención.
El “uso” y la “mención” en Frege tiene su correspondencia en MENTAL:
Uso: x, que hace referencia al contenido de x, a su evaluación.
Mención: x°, que hace referencia a la propia expresión x.
Por ejemplo, a+b puede hacer referencia a 7 (si a=3 y b=4). Y (a+b)° hace referencia a (a+b).

Las primitivas lógicas

Condición.
Frege utiliza el modus ponens como única ley para derivar inferencias.

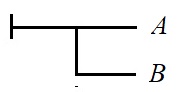
En MENTAL, el modus ponens se utiliza como lógica de implicación o como lógica de decisión. La distinción se basa en que se utilice o no dentro de una expresión genérica, respectivamente. En su forma genérica permite derivar conclusiones de modo automático. La notación MENTAL es lineal y más simple: (A→B), que indica “Si A, entonces B”.
Negación.
La negación lógica en MENTAL es una operación derivada, basada en el metaoperador “Contrario”.
Igualdad.
Frege utiliza el símbolo “≡”.

En MENTAL, el símbolo “≡” indica equivalencia, que es un concepto idéntico al de igualad de Frege. El símbolo “=” indica sustitución.
Definición.
La definición en Conceptografía es una primitiva: ||—A≡B

En MENTAL, esto se interpreta como que A representa a B y se expresa como (A =: B).
Generalidad.
Frege definió el cuantificador universal. El ámbito de un cuantificador universal es todos los objetos, la clase universal. El cuantificador existencial se deriva del universal y de la negación. Para Frege, el cuantificador existencial es un concepto de segundo nivel.

En MENTAL, la generalidad no está solo asociada a expresiones lógicas. La cuantificación universal se expresa en una expresión genérica, que puede ser de cualquier tipo. No hay un operador específico para la cuantificación. Las variables genéricas se expresan en negrita.

En MENTAL, el cuantificador universal va asociado a los parámetros de una expresión genérica. El ámbito de un cuantificador universal es la expresión genérica en la que está incluido. El cuantificador existencial es una expresión derivada, como afirmaba Frege. ∃xPx se define así:
(el número de elementos que tienen la propiedad P es mayor que cero). Esta expresión tiene la ventaja de que puede especificarse el número de elementos que cumplen la propiedad P. Y la no existencia ¬∃xPx se expresa como
Esta posición común se alinea con la visión de Kant que afirmaba que “existencia” no es un predicado real. En efecto, la existencia es la base de toda entidad, de la que sí se predica.

Ejemplos de expresiones lógicas

Notación de Frege
Notación moderna
MENTAL

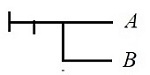¬(B → A)
(B → A)'

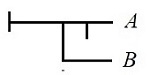(B → ¬A)
(B → A')

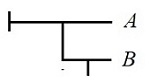¬B → A
(B' → A)

A → (B→ C)
A→ (B→ C)

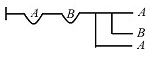∀A ∀B (A → (B → A))
⟨A → (B → A)⟩

Expresiones cuantificadas

La tabla siguiente compara sentencias generales en la notación de Frege, en la notación moderna del cálculo de predicados y en la notación MENTAL.

Ejemplo
Notación de Frege
Notación moderna
MENTAL

Todo es mortal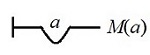

∀xMx
⟨x/M⟩

Algo es mortal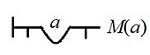

¬∀x¬Mx eq. ∃xMx
{⟨(x ← x/M)⟩}#>0

Nada es mortal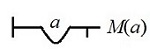

∀x¬Mx eq. ¬∀xMx
{⟨(x → x/M)⟩}#=0

Toda persona es mortal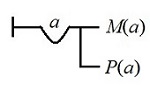

∀x(Px → Mx)
⟨( x/P → x/M )⟩

Alguna persona es mortal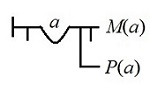

¬∀x(Px → ¬Mx) eq. ∃x(Px ∧ Mx)
{⟨( x ← x/P ← x/M )⟩}#>0

Ninguna persona es mortal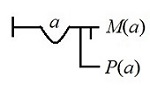

∀x(Px → ¬Mx) eq. ¬∀x(Px ∧ Mx)
{⟨( x ← x/P ← x/M )⟩}#=0

Todas y solo las personas
son mortales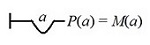

∀x(Px ↔ Mx)
⟨( x/P ↔ x/M )⟩

Conclusiones

El autor de esta obra considera que para concebir MENTAL ha realizado un “viaje” similar al que hizo Frege, y que existen notables paralelismos entre la Conceptografía y MENTAL:

Frege creó la Conceptografía buscando los fundamentos lógicos de la aritmética. Posteriormente se dio cuenta que el lenguaje que había ideado era universal, que valía para todas las ciencias, en especial para las ciencias formales.

MENTAL fue concebido inicialmente como un lenguaje informático, más concretamente como lenguaje de especificación y lenguaje multiparadigma de programación. Posteriormente, por su supremo nivel de abstracción, el lenguaje era aplicable a la matemática y a todas las ciencias formales en general. Y finalmente que era una “teoría (y práctica) de todo”.
Ambos son lenguajes platónicos que intentan realizar el sueño de Leibniz de crear un lenguaje universal para la ciencia (Lingua Charasteristica Universalis) y que sirva para realizar razonamientos como cálculo (Calculus Ratiotinator).
Frege se intentó apoyar en la lógica, pues consideraba que era la ciencia más fundamental. Fracasó porque la lógica es solo una dimensión profunda de la realidad.

MENTAL se fundamenta en los arquetipos primarios, de los que la lógica forma parte.
Para Frege, la Conceptografía era la formalización del Tercer Mundo, el mundo de los conceptos y entidades de tipo lógico (objetivo y atemporal). MENTAL es el lenguaje universal para la formalización del Tercer Mundo fregueano, pero concebido como el mundo de las expresiones de los arquetipos primarios.
Frege concibió la Conceptografía como un lenguaje analítico. MENTAL es un lenguaje sintético y analítico, siendo lo sintético el fundamento de lo analítico.
Frege utilizó como única regla de inferencia el modus ponens. MENTAL solo utiliza la primitiva “Condición”, que es también modus ponens, pero no el sentido de valores de verdad, sino de valores existenciales.
Frege utilizó axiomas lógicos. MENTAL utiliza axiomas semánticos (las primitivas semánticas universales) y axiomas generales que relacionan las primitivas.

Adenda
Más sobre Frege y la Conceptografía

El término “Begriffsschrift” no es original de Frege. Fue utilizado por primera vez por Franz B. Květ en 1857 y por Friedrich Adolf Trendelenburg en 1867. Estos dos filósofos alemanes pensaban, igual que Leibniz que el lenguaje natural era impreciso, inadecuado e insuficiente para el análisis de los temas filosóficos y científicos, por lo que era necesario crear un nuevo lenguaje de signos −siguiendo la idea de la Lingua Characteristica Universalis de Leibniz−, libre de influencias psicológicas, en el que las estructuras de signos reflejasen las estructuras de los conceptos, que los signos fueran independientes de lo sensible y enlazaran de forma directa y sistemática con los contenidos objetivos de los conceptos, y no con contenidos subjetivos. No obstante, el término “Begriffsschrift” se asocia con Frege, por el impacto que tuvo en lógica y filosofía la publicación en 1879 de su Conceptografía.

Frege fue acusado en su época por Ernst Schröder de haber creado, no un lenguaje universal (como prometía su título) sino solo un Calculus Ratiotinator, cuya tarea ya había sido realizada por Boole. Frege replicó que su lenguaje era una verdadera Lingua Characteristica y que el cálculo lógico era un componente necesario de dicho lenguaje.

En su tiempo, el trabajo de Frege en lógica apenas tuvo repercusión, llegando incluso a tener que publicar a su costa su última obra “Las Leyes Básicas de la Aritmética”. En la universidad de Jena –donde enseñaba matemáticas– se llegó a afirmar sobre su obra que “carecía de interés para la universidad”.

Pero en 1903, Russell incluyó un apéndice en su obra “Los Principios de las Matemáticas” en el que comparaba sus ideas con las de Frege. También las ideas de Frege se difundieron a través de los escritos de su estudiante Rudolf Carnap y otros estudiosos de su obra.

Wittgenstein reconoció “la gran obra de Frege” y su influencia en el estilo de sus sentencias lógicas. El Tractatus contiene 17 menciones a Frege, algunas de carácter crítico.

El trabajo de Frege tuvo una gran influencia sobre trabajos posteriores, entre ellos, la formalización de Principia Mathematica de Russell y Whitehead, la teoría de las descripciones de Russell, la teoría de la verdad de Tarski y el teorema de incompletud de Gödel.

Bibliografía

Dummett, Michael. Frege: Philosophy of Language. Harvard University Press, 1993.
Dummett, Michael. The Interpretation of Frege´s Philosophy. Harvard University Press, 1987.
Dummett, Michael. Frege and Other Philosophers. Oxford University Press, USA, 1993.
Frege, Gottlob. Conceptografía. Los Fundamentos de la Aritmética, Otros Estudios Filosóficos. UNAM (Universidad Nacional Autónoma de Mexico), 1972. Disponible en Internet.
Frege, Gottlob. Estudios sobre semántica. Ediciones Folio, 2003.
Frege, Gottlob. Ensayos de semántica y filosofía de la lógica. Tecnos, 1998.
Frege, Gottlob. Escritos filosóficos. Crítica, 1996. (Incluye Los Fundamentos de la Aritmética.)
Frege, Gottlob. Investigaciones Lógicas. Tecnos, 1984.
Frege, Gottlob. Lógica y semática. Univesidad Católica de Valparaiso (Chile), 1972.
Kenny, Anthony. Introducción a Frege. Cátedra, Colección Teorema, 1997.
Kneale, William y Martha. El desarrollo de la lógica. Tecnos, 1980.
Korte, Tapio. Frege’s Begriffsschrift as a lingua characteristica. Synthese, Oct. 2008. Dispomible en Internet.
Thiel, Christian. Sentido y referencia en la lógica de Gottlob Frege. Tecnos, 1972.
Stepanians, M. Gottlob Frege: una introducción. College Publications, 2007.